downloadnero.blogg.se - Insertion sorty

The current key is now at the right position. We keep on doing this, until j becomes equal to zero, or we encounter an element which is smaller than the key, and then we stop. Then using the while loop, we iterate, until j becomes equal to zero or we find an element which is greater than key, and then we insert the key at that position. We took a variable key, in which we put each element of the array, during each pass, starting from the second element, that is a. Now let's try to understand the above simple insertion sort algorithm. calling insertion sort function to sort the array We continue to move towards left if the elements are greater than the key element and stop when we find the element which is less than the key element.Īnd, insert the key element after the element which is less than the key element.īelow we have a simple implementation of Insertion sort in C++ language. Let's consider an array with values īelow, we have a pictorial representation of how bubble sort will sort the given array.Īs you can see in the diagram above, after picking a key, we start iterating over the elements to the left of the key.

And we go on repeating this, until the array is sorted.

Then, we make the third element of the array as key and will compare it with elements to it's left and insert it at the right position.

If the key element is greater than the first element, then we insert it after the first element.

If the key element is less than the first element, we insert the key element before the first element.

We compare the key element with the element(s) before it, in this case, element at index 0:.

The key element here is the new card that we need to add to our existing sorted set of cards(remember the example with cards above).

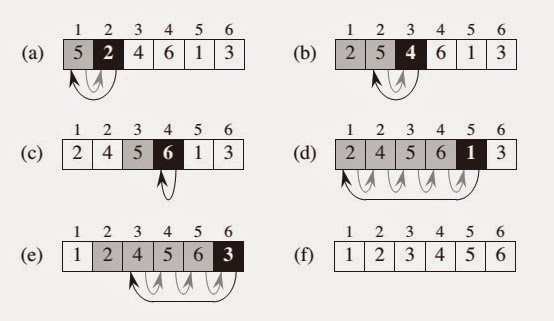
We start by making the second element of the given array, i.e.It is a stable sorting technique, as it does not change the relative order of elements which are equal.įollowing are the steps involved in insertion sort:.Like bubble Sort, insertion sort also requires a single additional memory space. It is better than Selection Sort and Bubble Sort algorithms.Insertion Sort is adaptive, that means it reduces its total number of steps if a partially sorted array is provided as input, making it efficient.It is efficient for smaller data sets, but very inefficient for larger lists.It starts from the index 1(not 0), and each index starting from index 1 is like a new card, that you have to place at the right position in the sorted subarray on the left.įollowing are some of the important characteristics of Insertion Sort: This is exactly how insertion sort works. Similarly, if more new cards are provided to you, you can easily repeat the same process and insert the new cards and keep the cards sorted too. Once you find the right position, you will insert the card there. Well, you will have to go through each card from the starting or the back and find the right position for the new card, comparing it's value with each card. If I give you another card, and ask you to insert the card in just the right position, so that the cards in your hand are still sorted. And they are sorted, or arranged in the ascending order of their numbers. Finally, the given array will result in a sorted array.Consider you have 10 cards out of a deck of cards in your hand.

Finally for 2, all the elements on the left side of 2 (sorted list) are moved one position forward as all are greater than 2Īnd then 2 is placed in the first position. Similarly with 5, as 7 (largest element in the sorted list) is greater

So, move 4 to its correct position, which is before 7. Now when on moving towards 4, 7 is the largest element Since 7 is the first element and has no other element to be compared with, it remains at its position. We will use Insertion Sort Algorithm, to sort this array: Shift all the the elements in sorted sub-list that is greater than the value to be sorted.īelow is an array of 4 numbers, which need to be sorted. Compare with all the elements in sorted sub-list.Ĥ. If it is the first element, it is already sorted.ģ. Insertion Algorithms: Steps on how it works:ġ. Values from the unsorted part are picked and placed at the correct position in the sorted part. The array is virtually split into a sortedĪnd an unsorted part. Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. However, they tend to come up a lot in computer science coursesĪnd theoretical explanations because they are often used as the naive approach, or the simplest implementation of sorting a collection. Most of the algorithms that we’ve been dealing with have been pretty slow, and seem inefficient.